Hallo zusammen,
der Thread ist zwar schon etwas angestaubt, aber der Titel passt
einwandfrei.
Auch ich habe mich schon längere Zeit mit dem Gedanken beschäftigt ob
es denn tatsächlich notwendig ist die komplette Tabelle (n. Tinseth) jeder
Berechnung zu
Grunde zu legen, beziehungsweise zwischen den fehlenden Meßwerten
abzuschätzen (linear interpolieren) oder sich gar an den vorgegebenen
Stw.
und Kochzeiten zu orientieren.
Ich wollte etwas wie f(Stw.(°P),T(min))= ?? % Ausnutzung Alphasäuren.
Da ich bis dato nicht fündig geworden bin hoffe ich das Rad nicht neu
erfunden zu haben!
Hier meine Lösung:
!Ich bitte die vielen großen Bilder zu entschuldigen, aber anders ist
glaube ich nicht viel zu erkennen!
Daher habe ich mir zunächst die komplette Tabelle skaliert -fehlende Werte
linear interpoliert - und erstmal
einfach nur draufgeschaut:
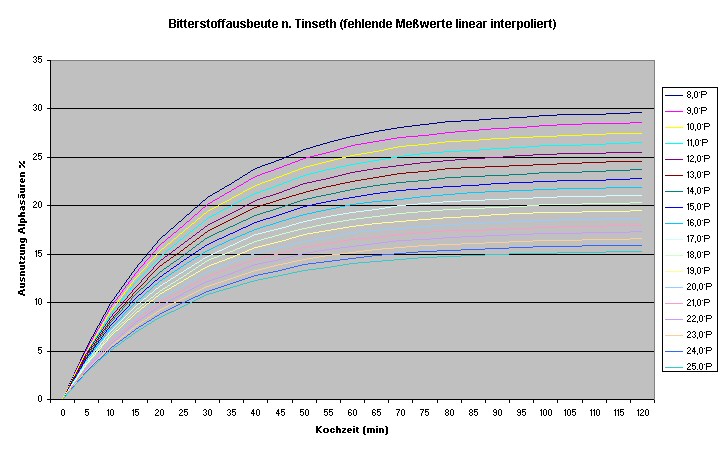
In Abhängigkeit von der Kochzeit kommen mehrere mögliche Funktionstypen in
Frage:
1) allgemeine Potenzfunktion mit Exponent zwischen 0 und 1
(Wurzelfunktionen)
2) allgemeine Logarithmusfunktion mit Basis > 1
3) allgemeine Exponentialfunktion
4) Polynom n-ten Grades
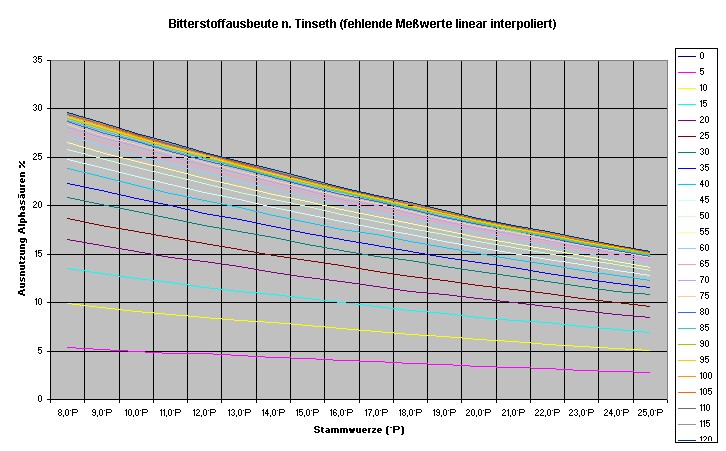
In Abhängigkeit von der Stammwürze kommen auch mehrere Funktionstypen in
Frage, um aber nicht allzuviel
probieren zu müssen habe ich mal kurz die y-Achse logarithmisch skaliert
und so war sofort zu sehen
das es sich um den obigen Typ 3 handelte (Werte f(x)=ln(y) liegen auf einer
Geraden).
Also blieb zunächst die Problematik welcher Funktionstyp für die Ausbeute
in Abhängigkeit von der Kochzeit
in Frage kommt. Als Lösungsansätze wählte ich die bereits vorhandene
lineare Interpolation (die mir allerdings
zu aufwändig ist, das sie dem Ablesen aus der Tabelle gleich kommt), ein
NEWTONsches Interpolationspolynom
n-ten Grades (n=Stützwerte-1) ermittelt nach dem Schema der dividierten
Differenzen (kurzes Java-Programm)
und der (willkürlichen) Festsetzung eines Grenzwertes (k=30) mit einer sich
daran annähernden allgemeinen Exponentialfuntion.
Das sieht im abschließenden Vergleich dann so aus:
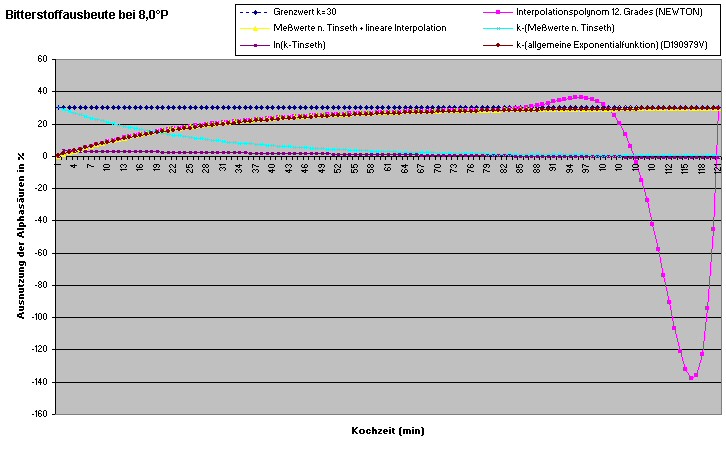
Damit steht fest das die Bitterstoffausbeute tatsächlich (wie viele
"natürliche" Phänomene) mit Hilfe einer sich k
annährernden allgemeinen Exponentialfunktion zu berechnen ist. Auch das
weitaus kompliziertere Interpolationspolynom
wäre bis gut 80 min Kochzeit noch brauchbar (Ich koche aber meißt länger).
Nach einigen Berechnungen erhielt ich schließlich folgende Formel:
Eine vollständig berechnete Wertetabelle führt zur abschließenden
Betrachtung:
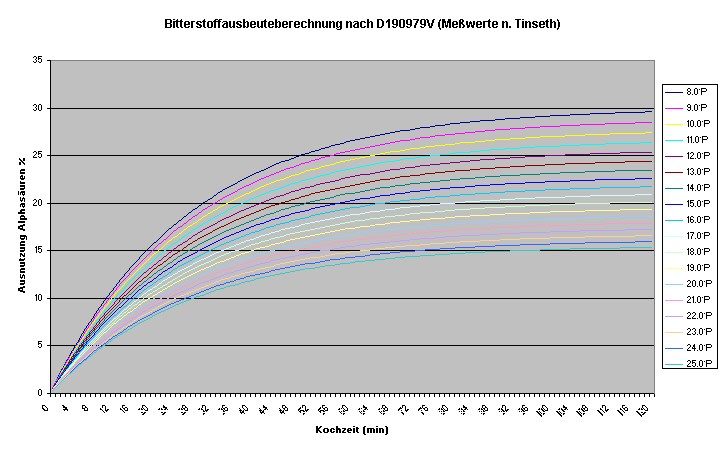
Schon allein der optische Vergleich zur (interpolierten) Grafik auf
Grundlage der Meßwerte von
Tinseth zeigt das die Formel im Bereich von 8°P-25°P und bei einer Kochzeit
von 0-120min
sehr genaue Ergebnisse liefert (wahrscheinlich sogar genauer als die
interpolierte Originaltabelle).
Jedoch stützen sich alle Formeln auf eine Handvoll Meßwerte deren
Genauigkeit für mich nicht
prüfbar ist (Während der Evaluierung der Formel sind mir einige
Meßungenauigkeiten/Streuungen in
der Tinseth-Tabelle aufgefallen). Da ich aber auch während des Würzekochens
nie eine konstante
Stammwürze beibehalten will und das Ergebnis auch immer noch von anderen
Faktoren abhängt reicht mir
diese Formel als Ergebnis meiner obigen Forderung. q.e.d.
Gruß Dominik
P.S.: Fehlermeldugen, Anmerkungen oder Kommentare sind natürlich erwünscht.
____________________
Wir wollen auch sonderlichhen dass füran allenthalben in unsern stetten
märckthen un auf dem lannde zu kainem pier merer stüchh dan allain gersten,
hopfen un wasser genommen un gepraucht solle werdn. - Un weizen.
Startseite
. Falls ich das gerade beim überfliegen
richtig gelesen habe sind seine
damit dürfte zumindest das nächste
Java-Programm klar sein...
